This article shows an interesting effect of dispersion whereby color components are progressively diverted from the spectrum, as in ‘fractional distillation’ or ‘fractional crystallization’ of liquids.
White Light & Rays
White light is composed of combined colors; different colors can be combined in appropriate intensities to produce white light. Each such white light is different from the other but the difference is not visible to the human eye. If you remove some source colors the combination of the others appears to be a new color.
Some analysts insist that a ‘ray’ is a single line of a single color (or ‘monochromatic’ light) and thus that there is no such thing as a ray of white light. Accordingly, what appear to be rays of white light in Fig.1 are really rays of different colors moving along the same line.
Diverting of Colors
When a ray of light hits the surface of a transparent material internally at an angle greater than the ‘critical angle’ it is reflected back inward; but if it hits at an angle less than critical it leaves the gem.
Each color has a different critical angle. This article will consider rays of only 3 colors – red, green, and blue at wavelengths given below; in diamond the critical angles of these colors are:
|
RED |
GREEN |
BLUE |
| wavelength (nm) |
640 |
520 |
440 |
| refractive index |
2.41 |
2.43 |
2.45 |
| critical angle |
24.5° |
24.3° |
24.1° |

Fig.1 Stone tilted 39° (43°from light source)
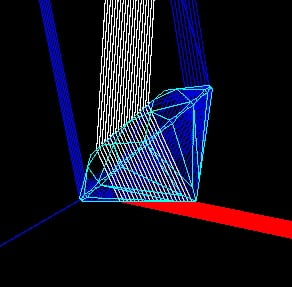
Fig.2 Stone tilted 41° per DiamCalc
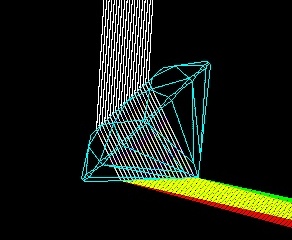
Fig.3 Stone tilted 43° per ‘DiamCalc’

Fig.4 Stone tilted 46° per ‘DiamCalc’
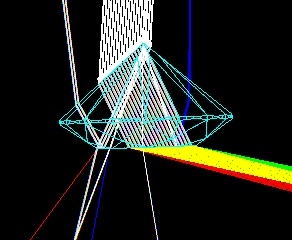
Fig.5 Approximate reverse of Fig 3.
Figure 1 shows a ‘Tolkowsky’ diamond tilted 39° per ‘DiamCalc’ software. Entering ‘rays’ (appear white) hit the first side of the pavilion at more than the critical angle of red light, so all three colors are reflected back to the crown.
Figure 2 shows the same diamond tipped 2° more; now the red rays hit at less than their critical angle and refract out of the pavilion, while the green and blue rays reflect back into the stone and exit through the crown (the blue here would be cyan if green intensity set lower).
IMPORTANT NOTE
These diagrams show paths of light coming FROM the viewer’s eye! This is the best way to study the paths of light relative to the viewer’s eye but it is important to realize that the various ‘exit’ angles shown are actually the directions of light SOURCES which would reach the viewer’s eye.
Figure 3 shows the stone tilted another 2°; at this position green rays refract, in addition to the red, producing what appears to be yellow light where they cross, although there is no yellow in the source! (so it is not monochromatic yellow)
Note the difference in exit angle for the two colors – we see only the red beyond one side of the crossing and only green beyond the other. The yellow appears only where they cross.
The blue rays are reflected back into the gem at this surface but do not show in this picture.
Figure 4 shows the stone tilted another 3°. Now all three colors – red, green and blue – are refracted from the same surface – but each at a different angle. Note that yellow appears where only the red and green rays cross (near lower edge), that cyan appears where only the green and blue rays cross (near upper edge) and that the light appears white where all three are crossing each other (green is in it).
IMPORTANT REMINDER
The divergence and combinations of color seen here are based on light emanating FROM the viewer’s eye.
On the other hand, if white light came from the direction of the red, green or blue rays shown here, only its component of that color would reach the viewer’s eye; this would appear as a flash of that color, changing to another color as the stone, light source or viewer moves.
One could say that the separate colors seen by the viewer are not due to separation in the gem of a single source of white light, but rather by sources of white light from various directions.
If, in Fig.3, the source was the collimated white light from above, and the viewer’s eye was at the lower right, the ‘wedge’ of yellow light formed by crossing of red and green would come to a point at a distance perhaps 10X the size of the gem and would not be visible to the viewer’s eye beyond that point! See also Fig.5.
This picture implies that light entering the pavilion can have desirable effects.
Bruce L. Harding 2006 Dec 05
Credits
These illustrations made with DiamCalc by OctoNus of Moscow, Russia. The multiple ray option was suggested by this author.
Probably most readers do not play with the multiple ray-tracing option offered in DiamCalc©. A lot of fun and education can be derived there. The article ‘Fractioning of Color by a Gem’, published in PriceScope this week is just one of many interesting studies using it.
I am using DiamCalc 2.3.0; there may be more recent ones. In this article I use Brilliant, which is default, from Cut/StandardCuts, then proceed with the following choices:
On the MenuBar hit Options / Model Type / Ray Trace / Multiple Rays from Eye.
You will see a side view wire frame illustration of the round brilliant with paths of multiple rays.
Look at bottom row of icons: at left end is Angle°, showing 5°.
To the right of this are three pairs of rotation controls; the pair at left tips the gem left or right.
Hit the right member of this pair 8 times, this will tip the gem 40° anticlockwise.
Then change Angle to 1° and hit the left member once to back up to 39°.
Now hit the right member again to duplicate the pictures illustrated here.
To change things, go to Options/Advanced/RaytracingOptions.
The examples of the article were made with the following default settings:
Color: Red, Green, Blue (they will mix properly to give white)
Ray width: 0.02 mm
Reflections: 5 (this is maximum number of reflections shown)
Minimal Intensity %: 50 (rays less than 50% intensity will not be shown)
When you change anything, hit Apply for it to happen.
Leave this menu on and watch the effects as you change things …
LIGHT SOURCE COLORS
Notice that many combinations of 3 or more colors can be mixed to produce white (the software chooses the appropriate proportions). It is interesting to see how these components separate/combine as you tilt the gem.
Seemingly incorrect separations/combinations can be explained if you reduce the Minimal Intensity that the illustration shows, but this can show so many rays as to be confusing.
SURFACE REFLECTION – an interesting illustration
This software can demonstrate surface reflection according to Fresnel’s law:
- tip the gem to about 45°,
- select 1 Reflection and any single light color, such as Red;
- for Minimal Intensity 20% or greater no surface reflection shows;
- at Minimal Iintensity 15% surface reflection appears.
– this means that surface reflection is between 15 and 20% …
- type-in 17 and 18% and note that it shows at 17 but not at 18%
– this means that surface reflection is between 17 and 18% …
- continuing, you will find that for Red light only it is between 17.7 and 17.8%;
- similarly, for Green light only it is between 18.0 and 18.1%;
- similarly, for Blue light only it is between 18.3 and 18.4%.
This is not important to the typical usage of DiamCalc but shows how powerful it can be as a teaching/learning tool.
B.L.Harding 2006 Dec 10