Fire and dispersion techy help please?

[Garry H (Cut Nut)]

Beryl and I have debated this before.
I have always thoguht that what goes in, must = what comes out. There fore I would expect if a ray of parallel light like this example , that we have been playing with recently on the MSU site, should show the same thing in reverse.

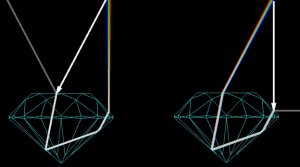
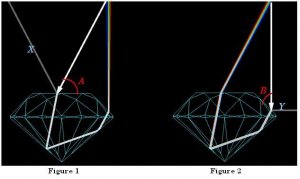
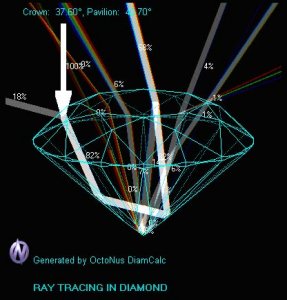
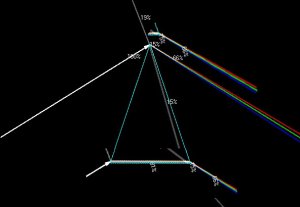
In playing with DiamCalc, it seems that the example on the right side (2) results in more dispersion.

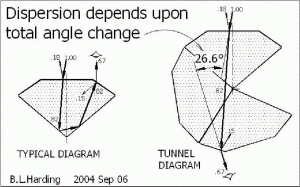
If I ramble on - the ray entering at a steep angle is dispersed more and then continues to be dispersed as it passes through the longer length of diamond. The ray on the left (1) is being dispersed mainly as it leaves the diamond, and therefore will be less dispersed because the distance travelled between the primary dispersion is less.

Let me try that another way:

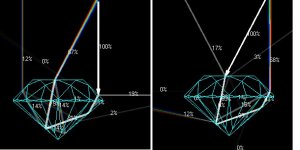
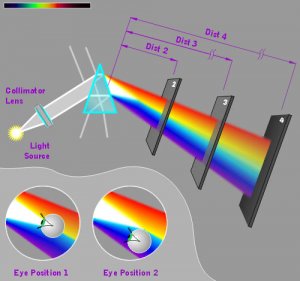
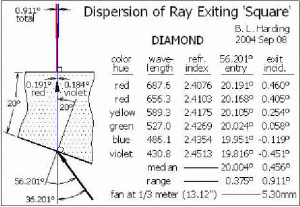
Stone (1) has about 7cm of dispersion distance from stone crown facet to top of my screen. Where as stone (2) travels through about 7cm of diamond then 7cm of air, before reaching the same approximate place.

Now if you view the diamond from 45cm away - this extra 7cm might not make much difference. But this seems to rip apart an idea that I have always assumed was right?

Any ideas folks?

 

[valeria101]

That's not a diamond, but a model of one. I surely have no idea about the ecuations there, but it should farely easy for whoever set them up to confirm whether the model takes into account your hypothesis ("what goes in must come out"). It may, or may not.

There is one detail in the picture that makes me think that for this particular model the sense of the light beam on any given trajectory DOES make a difference.

Here's what I see:
- the angle of incidence of the two beams is not the same (angle A is not equal with B)
- the reflected part of the incident beam is not as "wide" (line X is thinner than line Y, a little).

Any such observation would be better made on the numerical output of the model rather than on a graphic, since there might be some error involved in rendering these results via a projection... And the variation you mention seems to be minute.

Not a "techie" here, of course.

 

[beryl]

Garry:
. When Dr. Clifford Meinel critiqued my article 'FacetingLimits', he introduced me to the 'tunnel diagram', with which I hope you are familiar. Sorry; I do not have time to illustrate just now; Sergey can explain.
. At that time, he said that dispersion was related to the TOTAL bending of the ray, regardless of path through the gem which is easy to see in such a diagram. That is, the angle between entry and exit in such a diagram. By that logic, the total dispersion will be the same in either direction.
. Your illustration, however, does illustrate my point that light rays are not reversible - compare the partial surface reflections (gray) at entry in both pictures. The partial internal reflections at exit are also different, though they do not show here. It is virtually impossible to recreate a reverse ray which performs exactly the same.
. Nevertheless the 'primary' ray, which shows here in white and color, will have the identical exit intensity (Sergey taught me that), and identical dispersion if Dr. Meinel is correct.

 

[Garry H (Cut Nut)]

Thanks Bruce.
So you are sure these two dispersive seperations are going to be identical (if I managed to get them shooting down the same primary tunnels)?

On this one I have included the power%.

 

[valeria101]

Not sure what exactly I am doing on this thread, other than the discussion sounds irrezistible.

But, it seem that one would obtain exactly the same output regardless of ray direction if the in and out trajectories are parallel (obvious case) or if all the support of internal reflections is contained in the same section plan (not so sure).

Eh, this is going to be fun this evening...

 

[beryl]

Garry:
. That is my understanding at this time.
. This means that the angle of color fan (from one specific wavelength to another) would be same in both cases. Of course, viewing distance affects width of fan at that distance and therefore range of it which enters pupil - which is one reason why we sometimes see only one color.
. The percent difference in distance to eye at a realistic viewing range is insignificant, and so is width of the spectrum, so difference you see in this close-up is not meaningful.
. That is why it is so important to have double image on the screen - that of the gem in relation to viewer as well as details within the gem. Remember this feature in my program 'GemRay'? Octonus added this to DiamCalc at one time; I hope it is still there.
. A difference in viewing the two rays could come by superimposed light from other sources - especially direct surface reflections. Also, my stereo studies show that the two eyes see different things, and this complex image could be different at each viewing direction of your example.
. I am puzzled by power difference 68% vs 67% in your illustration; I suspect it is a minor round-off difference in the software. Perhaps Vladimir will explain.
. Today is holiday, so perhaps I will have time to make illustation of tunnel diagram for benefit of others reading this thread.

 

[beryl]

. Here is diagram for Tolkowsky diamond. Sorry it is so big. Also sorry for delay - Evelyn called me to breakfast.
. Angle is sum of complements to angles labeled by Valeria101 = 180°-A-B. Note to Valeria101: your angles A and B are not 'angles of incidence', but rather the complements to them. That is, angles of incidence are (90°-A) and (90°-B).

 

[strmrdr]

This brings to mind one of the experments we did in school with lasers.
Im not sure that 12 years later I can explain it.
But it has to do with the angle of the RI change as it goes from one material to another.
The angles are not the same coming from the back than from the front when reversing the path they are actualy opposite of each other.
Also you run into good old an object in motion tends to stay in motion and the light when it is at its fastest has a greater desire to drill right thru and not be bent. This comes into play with the offen ignored partical stream property of light.

Also keep in mind that the facet junction areas have a far greater affect on fire and dispersion than any other factor in a cut diamond as shown by the extra facet cuts that are getting more common.

My somewhat hazy memery 2c :}

 

[wanderlost]

Gary,

I find it interesting that I was playing with a very similar diamond in Diamond Calc on Friday & had my ray entering in an almost identical manner. My goal was to come up with the 'messiest' light diagram possible to emit as much fire & scintillation as possible (sounds familiar!)

... with minimal loss due to reflection or leakage...

I've attached one of my favorite light diagrams which mimicks yours quite closely. I'm not sure if it's particularly helpful, but I feel it's quite interesting at least.

 

[wanderlost]

here is the file now....

 

[wanderlost]

Gary...

I hope I'm not reading too much between the lines (and letting (Schrodinger's) cat out of the bag/box).... but I wonder a bit about the stone you've modelled... HCA 2.1, G/X/X/X - 57.1% depth, 60% table, 34° crown angle, 40° pavilion angle... which would explain why your Diamond Calc light trace looked a little goofy to me...

An interesting stone falls outside of any sort of reasonable AGS cut grade (something that I care for myself).... and would likely be ABSOLUTELY stunning in every light condition (as pertains to fire & scin)... but wouldn't a stone slightly different like: 57.9% depth, 60% table, 34° crown angle, 40.5° pavilion angle (0.9 HCA X/X/X/X) be more interesting to model? (In fact.... it'd be interesting to do a lot of things with & if anyone has this second theoretical stone for sale, drop me a PM

)....

 

[wanderlost]

One last post (I'm having too much fun with the Cut Study Modeller & need to get some work done)...

this is a fun Frankenstein here... the HCA hates it, but the fire *WOW*..
Step 1
Girdle 1
G. Thick 1.2
C.H. 19.84
C.A. 42.6
T.D. 59.33
Pav.D. 42.83
Pav. A. 39.94
Low. fac. 35

might not do much for white light but pretty neat otherwise

 

[Garry H (Cut Nut)]

Thanks Beryl.
The 67% - 68% difference is because I have a very slight modelling difference, and yes it will be magnified by rounding.
The images do not show as much dispersion 'to the eye' as the 'from the eye'. This confused me. Are you sure there is nothing to do with when the most dispersion happens - entering or departing the stone?

BTW the two images are still there on the latest version of DiamCalc.
Wonderlost - I think you might be lost

. My model has a 45 degree crown - I am not attempting to make a desirable stone - only to study a phenomena.

This image from MSU OctoNus shows a ray being dispersed by a prism. This almost never happens in real life - since most light does not travel in parallel rays. Beams of radiating light cause a very different effect. GIA made a big mistake in this respect in their 2001 Fire paper.

 

[Garry H (Cut Nut)]

Here is what happens to a beam.

 

[wanderlost]

Sorry about that Gary... I thought your settings for that stone were set in the Cut Study Computer when clicking on the link (that's where I got those numbers from)....


I think I may have jumped in a little too early and apologize, however, are you looking at dispersion & fire to correct GIA's paper (as the sun is not a parallel light source) with one of your key points being the rarer occurance of 'green fire/scin' vs. the other colors?

Also, should the reflected light in your first diagram (whereas in your second diagram it is diverted perpendicularly) be taken into account due to the mirror effect that would be observed by the viewer (which would obscure a portion of the colored light that would be visible)?

Finally, in the modelling software (and in your diagrams above), are you looking for maximum dispersion with a minimum of additive color? (for example: C.A.= 45, P.A.= 30.83 & table= 55.23)?

Hope I'm not making a nuisance of myself....-W

 

[Garry H (Cut Nut)]

That's OK WL.

Yes part of what I am doing is an analysis of GIA's approach.

The ray reversal in my first post was part of an ongoing discussion that some of us have had running for many years.

I like to get some discussion going about such things because it helps to clarify it in all our minds.

GIA should try it and save a few million dollars here and ther

 

[beryl]

Garry:
. APOLOGY time ...
. Out of curiosity, I calculated the dispersion of a ray going two ways through the same 20° wedge of diamond - entering 'square' and leaving at an angle and entering at that angle and leaving 'square'.
. There is a significant difference - a 1.54° fan the first way (= 9mm wide at 1/3 meter) vs. .91° fan the second way (= 5mm wide at 1/3 meter).
. Perhaps I misunderstood Dr. Meinel incorrectly in 1975 or made an error now. I will check my work and clean-up the illustrations to submit here asap.

 

[Garry H (Cut Nut)]

Very interesting dear Beryl, very interesting.


But surely you mean it the the other way around - more dispersed after entering at an angle and leaving square?

 

[Garry H (Cut Nut)]

You are right - passing a ray through a larger length of diamond does not increase the amount of dispersion.
Here i fired a ray thru the tip, and then thru the wider base of this prism.
Both entry and exit angles are the same. I expected the one passing thru the base to be more dispersed. Not so!
The dispersion happens on exit fara more so than one entry.

 

[beryl]

Garry:
. Here is 1st of 2 pics. 36.201° is the total bend described by Dr. Meinel.

 

[beryl]

... and here is 2nd.
. Diamond RI data are from "Dana's System od Mineralogy", Vol. 1, p.148 (7th Ed., 1944, John Wiley & Sons, New York/London/Sydney).
. I feel that I have made an error somewhere; I will think about it more. If it is not wrong, it adds fuel to my fire that "light is not reversible".
. Lets hope that Jose offers some comments.
. Thank you for the stimulus; my gem brain was sleeping.
PS: What's this "Dear Bruce" stuff? It may give someone a wrong idea.

 

[Paul-Antwerp]

Hi Bruce, good to see that someone woke you up of your summer sleep.

Garry, you are always around, but it is fun to see how you stir things up every now and then.

Anyway, I may be totally off, but it seems that you are carried away. Let me explain.

In one example, you have a white ray of light entering through the crown, resulting in a dispersed ray of light, leaving through the table.

In the other example, you try to reverse the ray by having a white ray of light entering through the table, resulting with a dispersed ray leaving through the crown.

I think that if you would study the reverse character of light, you should have a rainbow of light entering through the table in the second example. This may of course be exactly what is incorrect with reverse-ray-tracing.

Guys, I am not the techy, who can analyse this, but if what I am thinking is bullocks, I am sure that Bruce will simply say that it is.

Curious about your reaction,

 

[Garry H (Cut Nut)]

He he he Paul.
Actually this is rather important.
It also helps explain why a lot of fire comes out of the table in well cut rounds.

I think princess get a lot of their fire from light that enters at low angles. (they have very little crown).

I have asked vladimir to check the calc's big tough Beryl

 

[Paul-Antwerp]

Garry, I know it is important, but you did not catch what I meant.

Take example 1: white light enters through the crown, dispersed light leaves through the table.

Then, you try to reverse the light, by having white light entering through the table. But actually, that white light is not the reverse. The reverse would be to have that dispersed rainbow entering through the table (if in any technical way possible), I think.

If so, does this mean that we found a flaw in the theory of reverse-ray-tracing?

Just tell me if I am totally off base.

Take care,

 

[strmrdr]

----------------
On 9/8/2004 4:34:50 PM Paul-Antwerp wrote:

Garry, I know it is important, but you did not catch what I meant.

Take example 1: white light enters through the crown, dispersed light leaves through the table.

Then, you try to reverse the light, by having white light entering through the table. But actually, that white light is not the reverse. The reverse would be to have that dispersed rainbow entering through the table (if in any technical way possible), I think.

If so, does this mean that we found a flaw in the theory of reverse-ray-tracing?

Just tell me if I am totally off base.

Take care,


----------------

interesting,
What your saying is the reverse would be sending the dispersed colored light in and getting the "white" beam out.
I agree but im also sure it would never happen.
I wish I could remember more of what I learned about this stuff and knew how much different laser light acts in the same situation.

 

[Garry H (Cut Nut)]

That reversal would work to some extent - shine colored light in those directions and it would be a white ray exiting - but again - it would not be 100% of what goes in would come out.

If 67.5% of incitent of fire light comes out the dispersed side - and you reversed it, then 67.5% of the dispersed rays would emerge out as the recombined white ray.

But this is not the issue - the issue is when does dispersion occur, and when does it occur the most - on the entry and exit - or really mainly on exit?

 

[beryl]

Hi, Paul; good to hear from you. I hope to visit you in Spring.
Did you get copy of pic of you and me in Moscow?
. Paul, you are correct. I did a dissertation on that exact thing in 'DiamondTalk' a year or more ago, in the process of trying to explain that light is not reversible. I call that reconstructing a white source from its spectral components = almost impossible to do, except by putting identical prisms back-to-back.
. But that is not Garry's question. He is asking if a ray passing through a gem in one direction is dispersed as much, at exit, as it is going the other way. I said yes, based on my understanding of what Dr. Meinel told me, but now, having performed the precise calculations, I see that it is not (unless the bending is the same at both ends, as Garry last-illustrated with his symmetrical ray through a prism).
. The illustrations Garry provided of spectra through prisms, by OctoNus, are interesting but the subject of a whole different discussion which I am sorry I mentioned (portion of spectrum within the size of viewer's pupil).
. Got any more fun problems, guys?

 

[Paul-Antwerp]

Hi Bruce,

Looking forward to your possible visit in spring. Please inform me about your schedule beforehand. I will make sure to show you the real interesting details of the city and of the industry.

By the way, I never saw that picture of the two of us. I hope that it is publishable.

As for Garry's question, now that I understand it, I think that it is clear that you cannot have the same result in both directions. If you take the example of a white ray entering perpendicularly into a crystal, you have no dispersion at entry, and you only have dispersion at exit. Now, if you reverse the direction, the original ray is not entering perpendicularly, thus already you have dispersion at entry, and this will only result in more dispersion at exit, because only one of the wavelengths will exit perpendicularly, and the others will not, thus the dispersion will be increased.

Basically, I am trying to understand what you are coming up with, so if I am wrong, please just tell me so.

Take care,

 

[beryl]

Paul: Your logic is good. I succumbed to the desire to prove it with numbers, using this simple example, to see if my understanding of Dr. Meinel was wrong.
. Sometimes the numbers tell us things we cannot not see with logic; we must listen to what they are telling us. In this case they did not; your common sense was correct.
. Send me your e-mail address and I will send you pic (by Mike Cowing, I assume). My e-mail is [email protected]

 

[beryl]

Garry:
. As you know, the image in a diamond face-up consists of three zones (as Mike Cowing has cited from Watermeyer) - the center in which we see table-to-table (T-T) rays, the rest of the table in which we see bezel-to-table (B-T) rays, and the bezel in which we see table-to-bezel (T-B) rays. There are no bezel-to-bezel rays in a typical brilliant-cut diamond.
. The B-T and T-B rays bend the ray path by essentially the same angle (as described at the tunnel diagram). The attached illustration of a Tolkowsky diamond (40.75°/34.50°) shows that this is about 44° for T-B (and also B-T) rays. We know that the total for T-T rays is 45° in a Tolkowsky diamond (that was his premise for the 40.75° pavilion).
. So there is little difference in total refraction of any rays in an 'ideal' diamond following the mains. The subject just discussed, however, indicates that the width of the dispersion beam is greater when light enters 'square' to a facet and leaves obliquely. This is unlikely in the face-up position because the head blocks entry square to the table and will not see rays that entered the bezel 'square'; so entry is oblique unless we are looking at the gem at quite an angle.
. So what does this tell us? Let's kick it around.