- Joined
- Aug 15, 2000
- Messages
- 19,086
beryl|1290386159|2774971 said:. Garry: I am unaware of this Hodgson thing. Reference, please.
Surley Bruce - if not then you will love it!!!
Visual optics.
He's a Scotsman. One of our member Wink has stayed with him
http://www.google.com.au/search?sou...y+alan+hodgkinson&spell=1&fp=695053830d8c4981

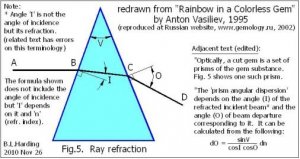

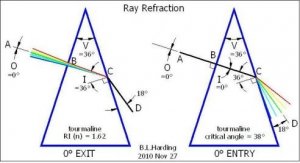
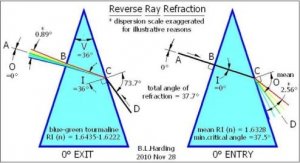
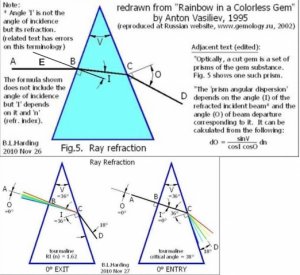

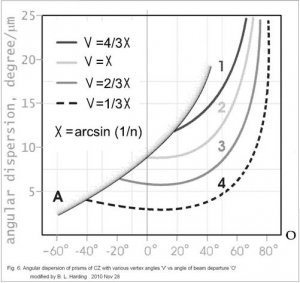










300x240.png)