stone-cold11
Super_Ideal_Rock
- Joined
- Sep 9, 2008
- Messages
- 14,083
Re: How important are HCA factor grades in assessing diamond
I have explained previously in another discussion we had. There is a simple, approximate hand calculation using high sch math. Those with DiamCalc will probably be able to generate one with better accuracy.
Using the parameters from this chart.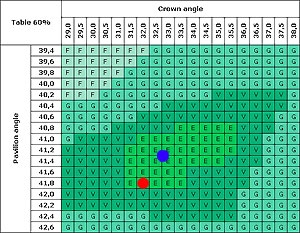
Your Example stone,
Stone A. Table 60, Crown 32.0, Pavilion 41.8.
Stone situated in the center of GIA Ex cut for 60% table,
Stone B. Table 60, Crown 32.5, Pavilion 41.2.
To simplify calculation, assuming the diamond is made up of conical shapes, no faceting, volume, V = 1/3 Pi R^2 H,
where, Pi = 3.142, R = base radius of cone, H = height of cone.
Volume of a cylinder, used for the girdle, = Pi R^2 H
This diamond is made up of the crown volume, pavilion volume and girdle volume.
The crown volume is obtained from the subtraction of 2 cones, the crown cone, everything above the crown, and the table cone, everything above the table.
Stone A
Crown cone.
Height of the crown cone = 50 * Tan(32) = 31.24
Volume of the crown cone = 1/3 Pi (50)^2 * 31.24 = 81795.21
Table cone
Height of the table cone = (60/2) * Tan(32) = 18.74
Volume of the table cone = 1/3 Pi (60/2)^2 * 18.74 = 17667.76
Pavilion Cone
Height of the pavilion cone = 50 * Tan(41.80) = 44.71
Volume of the pavilion cone = 1/3 Pi (50)^2 * 44.71 = 117037.83
Girdle
Volume of the girdle = Pi (50)^2 * 3 = 23561.95
Total volume of Stone A = 204727.22
Depth = 60.2%
Stone B
Crown cone.
Height of the crown cone = 50 * Tan(32.5) = 31.85
Volume of the crown cone = 1/3 Pi (50)^2 * 31.85 = 83392.30
Table cone
Height of the table cone = (60/2) * Tan(32.5) = 19.11
Volume of the table cone = 1/3 Pi (60/2)^2 * 19.11 = 18012.74
Pavilion Cone
Height of the pavilion cone = 50 * Tan(41.20) = 43.77
Volume of the pavilion cone = 1/3 Pi (50)^2 * 43.77 = 114594.01
Girdle
Volume of the girdle = Pi (50)^2 * 3 = 23561.95
Total volume of Stone A = 203535.53
Depth = 59.5%
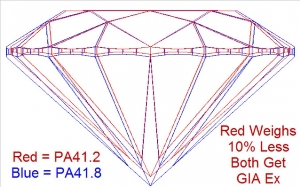
By Ratio, given original stone has a weight of 4.36carat, Stone B should weigh about
4.36/204727.22 * 203535.53 = 4.33carat, so about 0.03 carat.
The extra depth is where the weight comes from.
Depth of Stone A = 60.2%, Depth of Stone B = 59.5%.
If the limit is due to the crown height, meaning the crown angle is fixed at 32 degrees, if given a pavilion angle of 41.4, with a largish lower half, the carat weight will approximately come up to 4.32 carat with a depth of 59.5%.
Rockdiamond said:John- your explanation makes all the sense in the world- and if we look at diamonds in bulk, it likely explains a lot of the poorly cut stones out there- and we all agree there are plenty. But the generalization seems not to work in all cases.
Back to weight retention and, the question of if the 4.36ct was too deep- a question to Garry and John ( again)
If there's extra weight on this stone, how does it manifest itself?
That is to say, given that there's sufficient crown and pavilion angle, and more than ample spread ( in fact excellent spread for the weight)- where is this extra weight?
How much should the diamond have weighed?
I have explained previously in another discussion we had. There is a simple, approximate hand calculation using high sch math. Those with DiamCalc will probably be able to generate one with better accuracy.
Using the parameters from this chart.

Your Example stone,
Stone A. Table 60, Crown 32.0, Pavilion 41.8.
Stone situated in the center of GIA Ex cut for 60% table,
Stone B. Table 60, Crown 32.5, Pavilion 41.2.
To simplify calculation, assuming the diamond is made up of conical shapes, no faceting, volume, V = 1/3 Pi R^2 H,
where, Pi = 3.142, R = base radius of cone, H = height of cone.
Volume of a cylinder, used for the girdle, = Pi R^2 H
This diamond is made up of the crown volume, pavilion volume and girdle volume.
The crown volume is obtained from the subtraction of 2 cones, the crown cone, everything above the crown, and the table cone, everything above the table.
Stone A
Crown cone.
Height of the crown cone = 50 * Tan(32) = 31.24
Volume of the crown cone = 1/3 Pi (50)^2 * 31.24 = 81795.21
Table cone
Height of the table cone = (60/2) * Tan(32) = 18.74
Volume of the table cone = 1/3 Pi (60/2)^2 * 18.74 = 17667.76
Pavilion Cone
Height of the pavilion cone = 50 * Tan(41.80) = 44.71
Volume of the pavilion cone = 1/3 Pi (50)^2 * 44.71 = 117037.83
Girdle
Volume of the girdle = Pi (50)^2 * 3 = 23561.95
Total volume of Stone A = 204727.22
Depth = 60.2%
Stone B
Crown cone.
Height of the crown cone = 50 * Tan(32.5) = 31.85
Volume of the crown cone = 1/3 Pi (50)^2 * 31.85 = 83392.30
Table cone
Height of the table cone = (60/2) * Tan(32.5) = 19.11
Volume of the table cone = 1/3 Pi (60/2)^2 * 19.11 = 18012.74
Pavilion Cone
Height of the pavilion cone = 50 * Tan(41.20) = 43.77
Volume of the pavilion cone = 1/3 Pi (50)^2 * 43.77 = 114594.01
Girdle
Volume of the girdle = Pi (50)^2 * 3 = 23561.95
Total volume of Stone A = 203535.53
Depth = 59.5%
By Ratio, given original stone has a weight of 4.36carat, Stone B should weigh about
4.36/204727.22 * 203535.53 = 4.33carat, so about 0.03 carat.
The extra depth is where the weight comes from.
Depth of Stone A = 60.2%, Depth of Stone B = 59.5%.
If the limit is due to the crown height, meaning the crown angle is fixed at 32 degrees, if given a pavilion angle of 41.4, with a largish lower half, the carat weight will approximately come up to 4.32 carat with a depth of 59.5%.





300x240.png)