- Joined
- Mar 1, 2022
- Messages
- 220
Hi, are these your answers for which you feel has more contrast or which your eyes like better?
I never did get back to you. I found that there is a lot of psychophysical literature on perceived brightness and contrast, and that I was well out of my depth. It seems that you are now doing a bit of research of your own.Thank you for the reference. Crikey! If I was a bit confused before, I’m totally confused now… But seriously, their concepts and pictures raise interesting and relevant issues that I will have to think about. I’ll get back to you if I come up with anything worth saying.
is this one of those eye puzzle type things? b/c the contrast looks the same in each to me
Thank you to everyone who responded!! This has been illuminatingI feel like I've learnt quite a lot from these responses!!
I haven't had time to write everything up yet, but I'll get to it soon!!
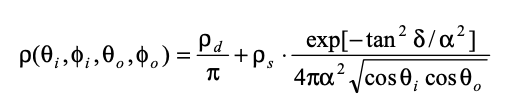


LOL. CIELab line in green, not orange. Posted a different plot (same topic just diff colours) and too late to edit.
And… Ignore the typos… Sorry y’all but you get what you pay for^^
I *wish* I’d had something I cared this much about in school, I might have actually paid attention!!
I'd die and go to heaven if I could get a degree in "General Jewelry Science"
I bet job placement would be low, though...
Curious, d'you use any of those sorts of devices? D'you trust them? I know the question of how much you can trust calibrations and measurements is a Big Topic in the diamond world. I wonder how a colorimeter would handle something like orient... I'd be very interested to learn more if that's something you do!Well, you could just buy a luminance meter or a colorimeter for colors if you want to measure the brightness of a pearl's surface or its color without having to guess
Finally got enough time to write up something coherent. This has been a fascinating and educational thought exercise. Thank you to everyone who played!!
I was trying to answer two questions, and I feel like now I've got a much better understanding of both
1. Can light coloured pearls ever be as "contrasty" as dark coloured pearls?
2. Do small pearls always look nicer than large pearls?
- - - - -
So... Well. Background first. Then discussion. Which in this fomat is a monologue so - moncussion.
A surface's reflectance depends on what that surface is made of and how smooth the surface is. On the one end of the scale there's a mirror. On the other end there's a rough matte surface (called "lambertian"). And a glossy, but not mirror, surface ("specular") is in between.
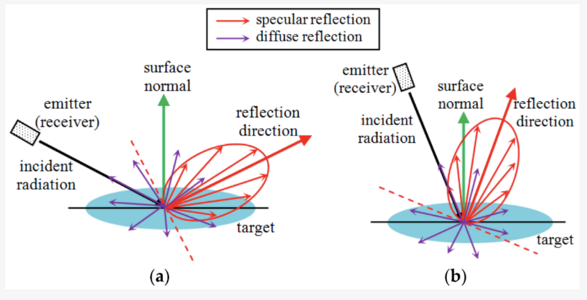
Awesome pic from paper [1] below. But sub the word "light" in instead of "radiation", and "spotlight source" instead of "emitter/receiver", and ignore the rest of the paper (the Phong model really doesn't work for this topic). Only part we want is this pic.
When light hits a totally rough/matte surface, one that has basically no glossiness, that light is reflected diffusely in all directions (purple arrows). This sort of surface is also called "lambertian". When light hits a glossy surface some of the light is still reflected diffusely (purple arrows), but a lot of it is reflected "specularly", at an angle equal and opposite to the incident angle (thick red arrow). Most of that specular reflection is dead on equal and opposite the incident angle, but some of it gets scattered a bit, creating a "specular lobe" (skinny red arrows).
A glossier surface creates crisper outlines of all reflected objects (fingers, cameras, noses, light spots)... The glosser the surface the less light that's diffused (lower energy represented by purple arrows) and the less the specular reflection is scattered (thinner specular lobe). If you're dealing with a ball bearing - say it's a perfect mirror - all the energy would be reflected equal and opposite incident angle and diffuse reflection would be negligible.
- - - - -
First question - Can light coloured pearls ever be as "contrasty" as dark coloured pearls. Discounting iridescence, my short answer is #No. Counting iridescence, my short answer is #Don'tKnow.
First component to body colour is just the plain ol' body colour. That part's easy, well-understood, and mathematically-provable. Y'all know how much I like my glossy surfaces. Let's talk about pearl nacre as a glossy surface. Say you've got two glossy surfaces, identical except that ones black and the other's white. I think we can all intuit that the black surface always just looks #Better. Right? Colours look more vibrant, everything is higher contrast. The glossy white surface can reflect just as precisely, where all the reflections have edges that are just as sharp, but compared to the black surface tones are always muted and washed out.
Turns out... This is our eyes, not physical thermodynamic reality, but it's literally everybody's eyes.
Physical thermodynamic reality first.
Ward's [2] model of light return from differently-coloured and differently-textured surfaces (he modelled paints) is three decades old, and a great many simulations (for video games and such) still use it. He coined the term Bidirectional Reflectance Distribution Function (BRDF), which is a fancy way to describe "the amount of light that's reflected in a specific viewing direction for a given incident light direction".
Why does direction matter? Well - it doesn't matter for rough matte lambertian surfaces. Diffuse light is reflected equally in all directions off the reflecting surface. But for glossy surfaces and mirrors, the position, size, and brightness of a reflection changes depending on where you are relative to the reflecting surface.
These papers [3][4] (they both cover basically the same topics) used a simplification of Ward's BRDF to model glossy white, grey, and black spheres. They plugged Ward's parameters in - [1] explains how he got these numbers, if anyone's interested. Here's the equation they used:
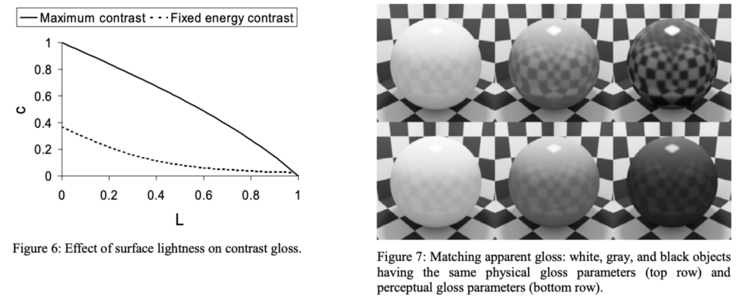
The paper explains that ρs values were (0.033, 0.066, 0.099), α values were (0.04, 0.07, 0.10), and ρd was set to (0.03, 0.193, 0.767; black, gray, and white) which are the diffuse reflectance factors corresponding to Munsell values (N2, N5, and N9). The black and white checks in the checkerboard surround were completely diffuse and had ρd’s of 0.03 and 0.767 respectively. By using all combinations of the ρd, ρs, and α parameters for the sphere objects, we produced the 27 images shown in Figure 1.
And here are the sphere models they created - that Figure 1 referenced above - these match our intuition about glossy black and white surfaces. And the red circles are mine, those are the spheres I'm most interested in:
In this equation, ρ(θi, φi, θo, φo) is the BRDF that we're solving for. This is a property of the sphere - the sphere's colour and surface texture. The background doesn't influence the sphere's BRDF in any way - background could be plain black, plain white, photos of trees, chessboard, doesn't matter. This model assumes that diffuse and specular reflection are independent. Which works fine for us.
ρd is the sphere's diffuse reflectance ability. So if the sphere was matte, not glossy, how much of incident light would that sphere reflect? This changes depending on whether the sphere is black, white, or grey - for black it's given as 0.03, for grey it's 0.193, and for white it's 0.767. So white spheres reflect more energy than black spheres.
α is a measure of how glossy the sphere is - how crisp and not-blurry reflected objects are. For the two spheres I'm interested in, I'm keeping α constant at a given constant 0.04.
ρs is the energy associated with light return from a glossy surface. More on this later, but for right now it doesn't matter - I only care about the red square spheres and this is given to us as 0.099 for both of those.
And a diagram of what that BRDF function ρ(θi, φi, θo, φo) is evaluating:
So... For my two spheres of interest... Presuming identical incident light direction and identical viewing direction eliminates δ, θo, and θi variance. And presuming identical glossiness and curvature of both spheres eliminates ρs and α variance. Which means the entire right term of the equation can drop out as a static. Which means that BRDF for white vs. black spheres varies directly with ρd/π... Which is a linear variance.
Okay. Remember that BRDF is a property of the white/black sphere. It has nothing at all to do with the background. What this is saying is... The amount of energy that's reflected (in a specific viewing direction, for a given incident light direction) off the white sphere is more than the amount of energy that's reflected off the black sphere. All objects that are reflected in the white sphere will show up lighter (brighter, whiter) than identical objects that are reflected in the black sphere.
And the total physical energy that can be reflected in this system (of white/grey/black spheres reflecting checkerboard squares) is bounded by "white checkerboard square reflected in white sphere" on the upper end, and "black checkerboard square reflected in black sphere" on the lower end. So
White square reflecting in white sphere (Ww) ~ 0.767/π * 0.767
Black square reflecting in white sphere (Wb) ~ 0.767/π * 0.03
White square reflecting in black sphere (Bw) ~ 0.03/π * 0.767
Black square reflecting in black sphere (Bb) ~ 0.03/π * 0.03
And Wb/Ww = Bb/Bw. Yup. Linear.
So, um, not what I was expecting. Clearly the white spheres look less contrasty than the black. So if white and black spheres are both reflecting white and black checkerboard squares with the same energy difference, why does the contrast between white and black reflections off the white sphere look lower than contrast between white and black reflections off the black sphere?
Rabbit, find hole.
This paper uses the CIELab lightness parameter as the basis for its explanation. I wasn't familiar with CIELab. Long story short for anyone else who doesn't recognize it - CIELab is a colour science philosophy, similar to RGB but, like, different. It's supposed to mimic what human eyes see during daytime. It's really old and really universally respected, and you can convert from CIELab to RGB and vice versa, for colour combination calculations - it's a whole seriously big and complicated #Thing.
I had to keep reminding myself that the Ward BRDF function models the energy that's actually being transformed through these reflection transactions. Those spheres in that model, those are intended to be renderings of physical reality. But what human eyes see isn't linear with energy transmission, and this has been known for a long time... My problem is just that I personally didn't know about itThis article [5] defines changing "lightness" as the equivalent of using a dimmer switch - Same color, just lighter or darker within the continuum of common hue and saturation/chroma.
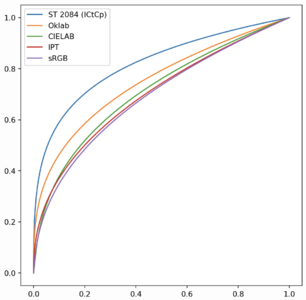
In the CIELab system, talking just about monochrome black/grey/white, the lightness value L* of diffuse white is 100 (sometimes 1.0), and the L* of diffuse black is 0 (always 0), and "mid grey" is 50. That's intended to represent what our eyes see, so "mid grey" is what our eyes interpret as being right between black and white. But what our eyes see isn't what's happening in terms of energy reflected off a coloured surface. Grabbed a simulation from [6], which shows the CIELab line in orange:
I deliberately didn't grab the units for the axes because the terminology they use is a bit different. The X-axis shows actual, real world, physical luminescence. Every increment from 0 to 1.0 on the horizontal represents a linear increase in luminosity of reflectance off a surface, from black to white. The Y-axis shows how our eyes percieve lightness changing from black to white as we go from 0 (black) to 1.0 (white) - the Y-axis is L*.
And where the orange line shows L* = 50, that "mid grey", that corresponds to 18% physical luminescence on the X-axis! Turns out this actually originated the 18% grey card that's ubiquitous in photography - funny, I never thought about where that 18% came from!!
So the fact that our eyes perceive lightness increases non-linearly is the explanation for why the white sphere looks less contrasty than the black sphere. Even though the actual phsyical difference in energy of black square vs. white square reflected is exactly the same for both white and black spheres. When we're looking at something dark, like the black sphere, our eyes register small differences in physical luminescence as being significant; when we're looking at something light it takes a much bigger change in actual luminescence for our eyes to note a difference. Exactly why our eyes behave that why, that's biology and beyond my interest, shrug
But here's the math behind that CIELab plot. In 1931 the International Commission on Illumination (Commission internationale de l'éclairage, CIE) determined these formulas for lightness:
Y = physical luminance of a reflecting surface
Yn = reference luminance of white (1.0)
L* = 903.3 ∙ (Y/Yn), where (Y/Yn ≤ 0.008856) (as in, really really close to 0)
L* = 116 ∙ ((Y/Yn)^1/3) – 16, where (Y/Yn > 0.008856) (for most of the plot)
If you graph these two equations they cross over at ~ L* = 8. So L* is a straight line from 0 to 8, and a cube root from 8 to 100. So in that plot the orange curve is a straight line from 0 to 0.08 up the Y-axis, and a cube root from 0.08 to 1.0 up the rest of the Y-axis.
And if you invert that second equation (for L* > 8 ) to compute Y as a function of L* and Yn,
Y = ((L* + 16) / 116)^3 * Yn
Solving this for L* = 50 and Yn = 1 yields Y = 0.18, 18% "mid grey"
Back to the original paper. They define ρd as the inverse function of L*. So they're asserting a direct commutation between ρd and L*. Sure. Keeping ρs and α the same between the two red-squared black and white spheres yields the dotted line plot below. So as L* increases linearly, the perceived differential between two L* values (contrast, c) decreases nonlinearly. Makes sense.
Figure 6 illustrates the influence of the diffuse component on apparent gloss. Here the solid curve plots the maximumcontrast gloss c achievable for surfaces with different lightness values (derived by enforcing energy conservation of theBRDF). This curve defines the envelope of gloss space with respect to surface lightness. We also plotted how contrast glossvaries with lightness for a fixed energy of the specular lobe. This curve shows that for the same specular energy, contrastgloss is smaller for lighter objects. That is to say, if two surfaces are painted with black and white paints having the samephysical formulations, the black surface will appear glossier than the white one.
So takehome? For two pearls of the same size that have exactly the same surface quality, if you could ignore iridescence, a darker-bodied pearl is always going to look more contrasty than a lighter-bodied pearl. If two pearls "look" like they have the same amount of contrast, but one is darker-bodied than the other, the lighter-bodied pearl must be objectively higher quality than the darker-bodied pearl... And the highest quality light-bodied pearl can never, ever look as contrasty as the highest-quality dark-bodied pearl.
I’ve personally seen this with both Tahitians and akoya. It’s easier to see in Tahitians IMO. Light-bodied tahitians are less contrasty than dark-bodied tahitians, even when the outlines of reflected objects are just as crisp. Totally true. Akoya... My blue akoya are more contrasty than my white akoya, and both have strong pink iridescence, but the blue have darker bodies. And I've also seen that darker-bodied white akoya are more contrasty than light-bodied white akoya with similar iridescence strength.
But that's really only half the story. Iridescence create an incredible amount of contrast and body colour be d*mned. I have a feeling that when it's a question of iridescence vs. less iridescence, "more iridescent" ALWAYS wins no matter what the body colour.
- - - - -
Second question - Do small pearls always look more "lustrous" than large pearls? This one kinda uses the answer to the first question as background.
According to the poll, some people define "contrast" as functions of both the difference between light and dark and how crisp the transition between light and dark is. And also how how big the area of black and white is, but we're talking about pearls which are all pretty small so, y'know. Not relevant. So - for some people "higher contrast" means both "blacker vs. whiter" and "less blurry boundary between light and dark". For other people "higher contrast" just means the first bit, and blurred edges don't matter. But for most people who responded to both of my questions, however they defined "contrast", they LIKED a more crisp transition better. Not everyone!! Which was eye-opening!! But yeah, most people.
Think about the back of a paperback book. It's usually low-key glossy. Maybe a bit scratched up. Shine a flashlight onto it. The reflected light spot (the "specular highlight") will be a circle with kinda blurry edges, and the brightness fades out away from the center of the light spot.
Bend the back of the book a bit - make the bend where the light spot is. The light spot will change shape - it'll go from circular to long and skinny. The more you bend the skinnier it gets. As in - the light spot becomes shorter perpendicular to the direction of the bend... And the area of blurriness emanating from the center of the light spot in that direction (perpendicular to fold) is gets smaller, which makes the transition between light and dark on that axis look more crisp. The surface hasn't changed at all, but the shape of the specular lobe changes with the angle of the reflecting surface relative to incident light.
Now take the back of the book off the book and turn it into a sphere. Somehow. The lightspot changes shape again - goes back to a circule. So same shape as when it was a flat surface. The specular lobe is smaller, though - the blurriness emanating from the center of the light spot is smaller, and the transition from bright to dark looks crisper in all directions...
The smaller you make the sphere the more quickly the brightness of the light spot transitions into darkness, and the more sharp the transition looks. Again, the material hasn't change a whit. And this is true not just for the light spot but of the blurring of all reflected objects...
Some people who responded to my poll would say that as the pearl gets smaller "contrast" improves (because reflection edge blurring decreases). I would say this too, by the way. Other people would say that "contrast" doesn't change. No right or wrong answer. But the fact that nearly everyone likes less blurring tells me that no matter how we define what we're seeing - glow, luster, contrast, sharpness - for the exact same pearl surface, for the same body colour, for the same strength of iridescence, a smaller pearl really does look better to nearly everyone!!
So if a bigger pearl and a smaller pearl look identically sharp/glowy/non-blurry/lustrous, then the bigger pearl's surface is actually higher quality than the smaller pearl's. The change isn't linear though - and the scale is asymptotic: The top of the specular reflectance scale is a mirror, and a small spherical mirror doesn't reflect more sharply than a large spherical mirror. Size has no impact on integrity of reflection from mirrors! Size actually makes the most difference with low-quality (less glossy) pearls - with two lower quality pearls, the smaller pearl will look significantly nicer than the larger pearl. Go up to the top of pearl surface quality (which is still a good ways off from being an actual mirror) and the smaller pearl will still look a bit nicer still no doubt, but it won't be that much nicer than the bigger.
More resources in the next section. Some of them actually model this but I'm out for the day. I just have to trumpet [7] again. It's such a good, easy read - such an easy way to #GetInto these topics, and I feel like I get something new out of it every time I read it. Once upon a time I got my MIL some GSS, and I absolutely fell in love with them - I remember saying that they looked like they had actual little lights inside them. Years and years later here's a journal paper that describes how pearls are quite literally lit from within, and I can't get over how romantic that is
- - - - -
[1] Tan, Cheng. 2017. Specular Reflection Effects Elimination in Terrestrial Laser Scanning Intensity Data Using Phong Model.
https://www.mdpi.com/2072-4292/9/8/853/htm
[2] Ward. 1992. Measuring and Modeling Anisotropic Reflection.
https://cseweb.ucsd.edu/~ravir/6998/papers/p265-ward.pdf
[3] Ferwerda, Pellacini, Greenberg. 2001. Psychophysically based model of surface gloss perception.
https://www.researchgate.net/public...cally_based_model_of_surface_gloss_perception
[4] Ferwerda, Pellacini, Greenberg. 2000. Toward a Psychophysically-Based Light Reflection Model for Image Synthesis.
[URL='https://www.researchgate.net/...ed_Light_Reflection_Model_for_Image_Synthesis[/URL]
[5] https://cdn-s3.sappi.com/s3fs-public/sappietc/Defining and Communicating Color.pdf
[6] https://raphlinus.github.io/color/2021/01/18/oklab-critique.html
[7] Ozaki, Kikumoto, Takagaki, Kadowaki, Odawara. 2021. Structural colors of pearls.
https://www.nature.com/articles/s41598-021-94737-w#Fig1
Other references:
Todd, Norman, Mingolla. 2004. Lightness Constancy in the Presence of Specular Highlights.
https://www.asc.ohio-state.edu/todd.44/date/Todd, Norman & Mingolla 2004.pdf
Olkkonen, Brainard. 2010. Perceived glossiness and lightness under real-world illumination.
https://jov.arvojournals.org/article.aspx?articleid=2191693
GIGILASHVILI, SHI, WANG, PEDERSEN, HARDEBERG, RUSHMEIER. 2021. The Role of Subsurface Scattering in Glossiness Perception.
https://graphics.cs.yale.edu/sites/default/files/mainsupplementary.pdf
Fan, Zhou, Myagkaya. 2021. Investigation of nacre nanostructure by analyzing its structural color pattern.
https://www.nature.com/articles/s41598-021-99327-4.pdf?proof=t+target=
Banks. Shape from Specularities.
https://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/AV0506/s0568337.pdf
https://www.scratchapixel.com/lessons/3d-basic-rendering/phong-shader-BRDF
Muhammad, Fujimura, Komaru. 2021. The effects of nacre microstructure on green and pink interference colors in Pinctada fucata martensii pearls.
No public link to this, but I've got download access and I'm attaching it here as a PDF because I think closed source literature is BS.
https://cielab.io/
This one is a FANTASTIC writeup on colour science philosophies (ie. What the heck does CIELab mean):
https://mathematica.stackexchange.c...e-mix-of-4-colors-defined-in-cielab-lab-model

If you use a camera with close-up ability and manual settings, a standard fixed lighting environment, and standard processing, you can at least read comparative luminance from the RGB values. You could compare different pearls and could compare different parts of the same pearl.Curious, d'you use any of those sorts of devices? D'you trust them? I know the question of how much you can trust calibrations and measurements is a Big Topic in the diamond world. I wonder how a colorimeter would handle something like orient... I'd be very interested to learn more if that's something you do!
Me, I have no more money to play with this year, sadly, it's all gone to sparklies and Starbucks and I don't really want to investigate that ratio too closely
You have certainly influenced me to take an interest in pearls.My social media presence is limited to PS but it's always gratifyingly awesome to hear that something one said or did inspired someone else in some way!!
Agree on the second and third making the pearls look bright and the fourth making them blah - the fourth is so zoomed in I didn’t even register that I was looking at the pearl lineup right away. Perspective…Thank you for this! It's a fair bit to digest. One key issue is how perceived brightness and contrast depend on scale.
Vermeer knew a bit about pearls, light and perception. Here is his Woman with a Pearl Necklace in successively increasing detail:
To my eye, in the 2nd and 3rd pics, the pearls look bright. In the last pic, which shows how the magic works. not so much. The trick is surprisingly (to me) simple: white highlights, ghostly grey body, shadow. But it works when viewed at the right distance. Note the in an oil painting, nothing can be objectively brighter that white. It's only tricky local contrast that can make it appear so.
We are trees in the same forest LOL. This is what got me started, from a convo with a friend - I tried to calculate contrast differential between light and dark reflections in light and dark pearls from the RGB channels in photoshop. My attempts failed pretty miserably though, because I couldn’t isolate that specular highlight (and surrounding blur) out, which of course our eyeballs do automatically. And the pearls I used also had… They didn’t have particularly strong overtones but for whatever reasons the blue component was sky high… I think I could do a better job now.If you use a camera with close-up ability and manual settings, a standard fixed lighting environment, and standard processing, you can at least read comparative luminance from the RGB values. You could compare different pearls and could compare different parts of the same pearl.
You have certainly influenced me to take an interest in pearls.
Curious, d'you use any of those sorts of devices? D'you trust them? I know the question of how much you can trust calibrations and measurements is a Big Topic in the diamond world. I wonder how a colorimeter would handle something like orient... I'd be very interested to learn more if that's something you do!
And thank you!!My social media presence is limited to PS but it's always gratifyingly awesome to hear that something one said or did inspired someone else in some way!!